반응형

https://www.acmicpc.net/problem/1937
1937번: 욕심쟁이 판다
n × n의 크기의 대나무 숲이 있다. 욕심쟁이 판다는 어떤 지역에서 대나무를 먹기 시작한다. 그리고 그 곳의 대나무를 다 먹어 치우면 상, 하, 좌, 우 중 한 곳으로 이동을 한다. 그리고 또 그곳에
www.acmicpc.net
dp[i][j]
i, j에서 갈 수 있는 최대 개수
DFS 핵심
①
현재 칸에서 다음 칸으로 이동: 1번
다음 칸에서 임의의 칸으로 이동: 최대 x번
∴ 현재 칸 -> 다음 칸 -> 임의의 칸: 최대 x + 1번
②
다음 칸의 계산이 이미 끝났을 경우 (visited = true)
-> 다음 칸의 값(dp[nx][ny])을 가져와서 계산
다음 칸의 계산이 안되어 있을 경우 (visited = false)
-> dfs(nx, ny) 수행 / return 값: 다음 칸의 값
|
1
2
3
4
5
6
7
|
// 계산이 끝났을 경우
if (visited[nx][ny])
dp[x][y] = max(dp[x][y], dp[nx][ny] + 1);
// 계산을 해야하는 경우
else
dp[x][y] = max(dp[x][y], dfs(nx, ny) + 1);
|
cs |
진행과정




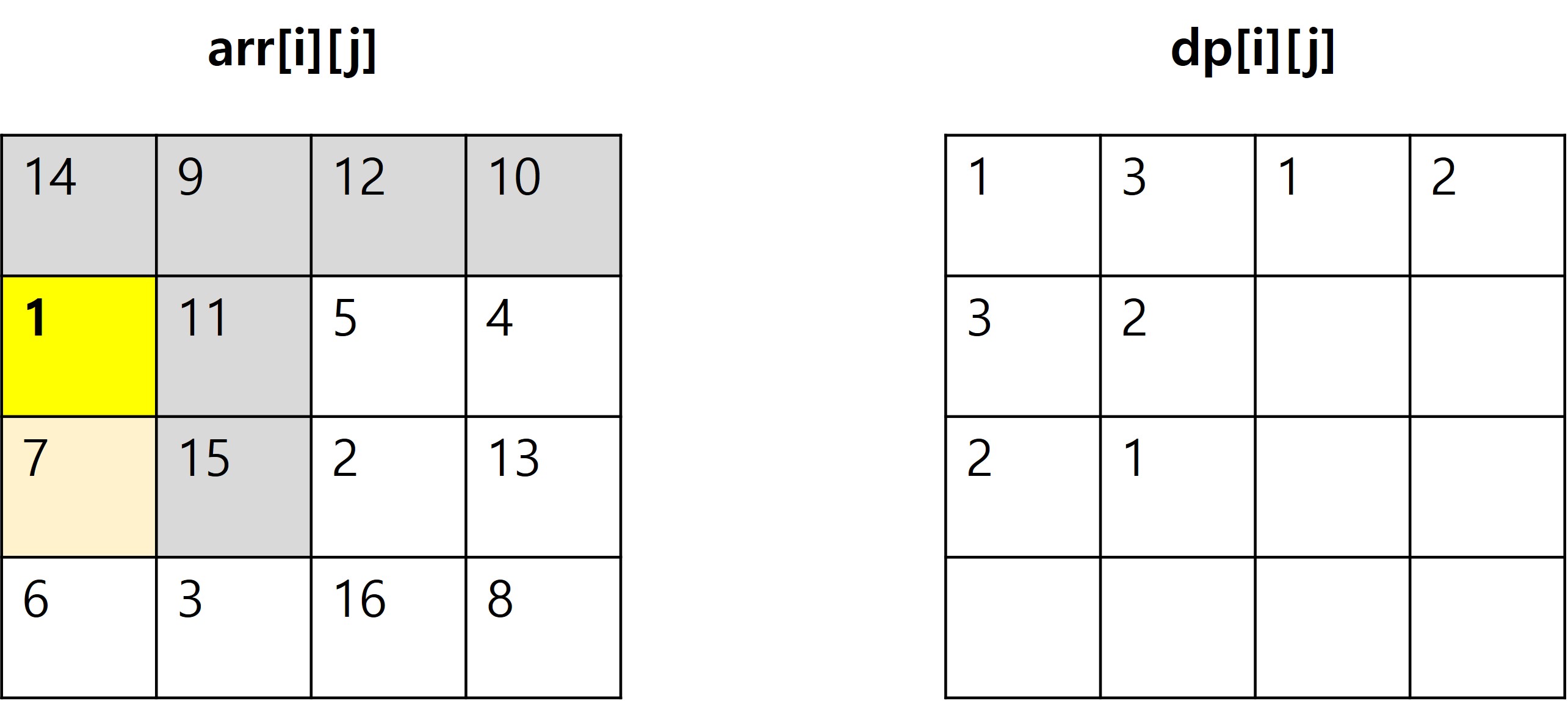





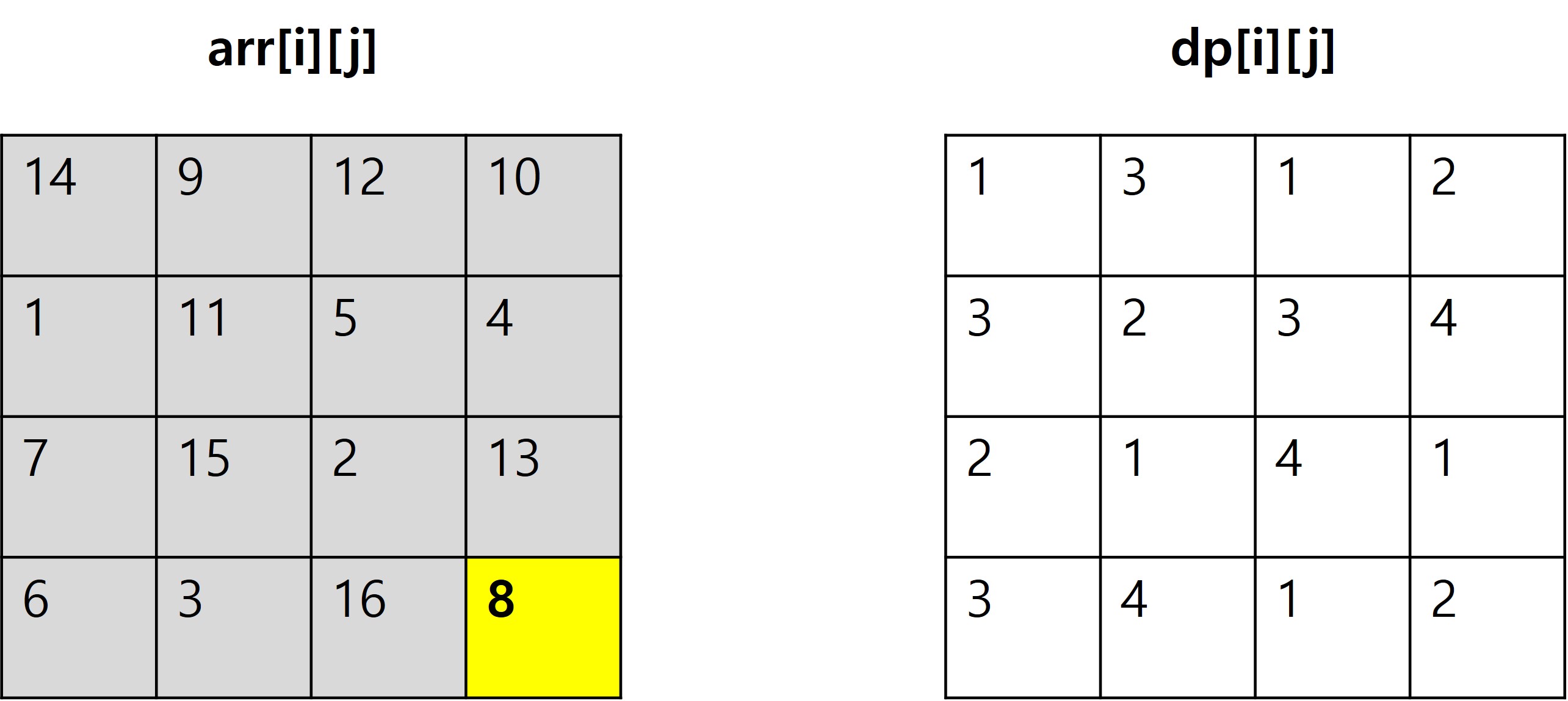
012345678910
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <iostream>
#include <algorithm>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
int dx[] = { -1, 0, 1, 0 };
int dy[] = { 0, 1, 0, -1 };
int ans, n, arr[501][501], dp[501][501];
bool visited[501][501];
// dp[i][j]: i, j에서 갈 수 있는 최대 개수
int dfs(int x, int y) {
visited[x][y] = 1;
dp[x][y]++;
rep(i, 4) {
int nx = x + dx[i];
int ny = y + dy[i];
// 이동 불가
if (nx < 0 || ny >= n || ny < 0 || ny >= n || arr[x][y] >= arr[nx][ny]) continue;
// 계산이 끝났을 경우
if (visited[nx][ny])
dp[x][y] = max(dp[x][y], dp[nx][ny] + 1);
// 계산을 해야하는 경우
else
dp[x][y] = max(dp[x][y], dfs(nx, ny) + 1);
}
return dp[x][y];
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin >> n;
rep(i, n) {
rep(j, n)
cin >> arr[i][j];
}
rep(i, n) {
rep(j, n) {
if (!visited[i][j])
dfs(i, j);
}
}
rep(i, n) {
rep(j, n)
ans = max(ans, dp[i][j]);
}
cout << ans;
}
|
cs |
반응형